
Irrational numbers in decimal form are nonrepeating, nonterminating decimals. An irrational number, on the other hand, cannot be written as a fraction with an integer numerator and denominator.
In decimal form, a rational number is either a terminating decimal (such as 2, 1.375, and –0.5) or a repeating decimal (such as 0.3333.). That is, a rational number is a fraction where a is an integer and b is an integer other than zero. A rational number is any real number that can be expressed exactly as a fraction whose numerator is an integer and whose denominator is a non-zero integer. We can further divide the real numbers into two distinct classes: rational numbers and irrational numbers. In the positive (right) direction, the real line extends toward +∞ (positive infinity) in the negative (left) direction, it extends toward –∞ (negative infinity). Note carefully, however, that infinity (typically written as ∞) is not a real number-it simply represents the fact that the real line extends indefinitely. What is illustrated above is a portion of the real line. Thus, we say that the real number line extends to infinity in both the positive and negative directions. Think of any number regardless of the number, you can always think of a number that is greater than or less than the one you chose. A coordinate point is shown for the number 1.5. For obvious practical reasons, not all real numbers can be shown, so we generally show coordinates for a subset of the real numbers (often, integers, but different situations call for different subsets). Below is an illustration of the real number line. The real number corresponding to a particular point on the line is called a coordinate. Every real number has a corresponding point on the line, and this line is generally drawn horizontally with the right-hand direction representing increasing value and the left-hand direction representing decreasing value. Thus, we can illustrate the real numbers using a number line-in this case, the real line or real number line.

Just as with the natural numbers that we learn first as children, the real numbers are ordered, which we can intuitively define as the concept that given a pair of unique real numbers, one of them is greater than the other (and, conversely, one is less than the other).

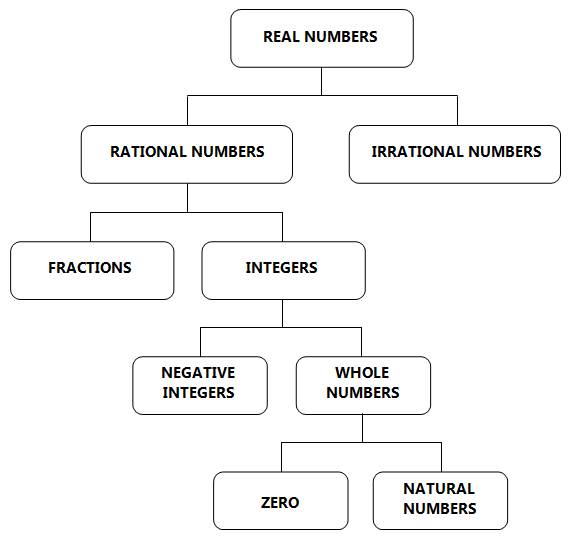
All of these numbers, including the integers and all possible numbers in between, are called the set of real numbers. We can also add negative values of the natural numbers, expanding our view to integers (., -3, -2, -1, 0, 1, 2, 3.), and finally all the intermediate numbers between any two successive integers (decimal values). As we gain a deeper understanding of numbers, we add the number 0, forming the whole numbers (0, 1, 2, 3.). When we first learn to count, we are learning an ordered set of numbers: generally, the so-called natural numbers (1, 2, 3.).


 0 kommentar(er)
0 kommentar(er)
